高校数学 - 図形

久しぶりに数学を復習しようと思い立ちました。この記事はそのメモです。またLatexで数式を書くための練習です。第21回は図形です。まずは高校数学で登場する定理を集めてみました。なお、次回はこの範囲の定義や証明を延々と… 大変だぉ。

今回はGeoGebraが大活躍です。たくさん図形を書いてずいぶんGeoGebraの練習になりました。これからもどんどん使っていきたいと思います。でもまだ立体図形はうまくかけないんですよね。もっと練習しなきゃ。

以下については記載されていなかったので、チャート式 数学 I+Aを参考に追記しました。

• 三平方の定理
• 三角形の五心、傍心
• トレミーの定理

• • • 教材
    • 図形の性質
      • 定理のまとめ

教材

• 新編 数学A 平成25年度用

編者: 高橋陽一郎
出版社: 啓林館
発行日: 2012-12-10
ISBN: ISBN978-4-402-03692-7
価格: C4341 ￥00000E

学習範囲 (目次より)
第3章 図形の性質

• 新課程 チャート式 数学I+A

編者: チャート研究所
出版社: 数研出版
発行日: 2013-02-01
ISBN: ISBN978-4-410-10172-4
価格: C4341 ￥1820E

学習範囲 (目次より)
数学A 第3章 図形の性質

図形の性質

定理のまとめ

[定理] 中点連結定理
$\triangle ABC$で辺$AB, AC$の中点をそれぞれ$M,N$とすれば
$$MN /\!/ BC \ かつ \ MN=\frac {1}{2} BC$$

[定理] 三平方の定理 (補)
$\triangle ABC$で辺$BC=a, CA=b, AB=c$とすると
$$\angle C = 90^{\circ} \iff a^2+b^2=c^2$$

[定理] 中線定理 (補)
$\triangle ABC$の辺$BC$の中点を$M$とすると
$$AB^2 + AC^2 = 2(AM^2 + BM^2)$$

[定理 1] 角の二等分線と辺の比
$\triangle ABCの\angle A$の二等分線と辺$BC$との交点を$D$とすると
$$AB:AC=BD:DC$$

[定理 2] 外角の二等分線と辺の比
$\triangle ABCの\angle A$の外角の二等分線と辺$BC$との交点を$D$とすると
$$AB:AC=BD:DC$$
となる。ただし$AB\neq AC$とする。

[定理] 定理2の逆 (補)
$\triangle ABC$の辺$BC$上の点$D$に対して$BD:DC=AB:AC$が成り立つならば$AD$は$\angle A$の二等分線である。

[定理 3] 三角形の辺と角の大小 (補)
$\triangle ABC$で
$(1)$ 大きい辺に対する角は、小さい辺に対する角より大きい。
$(2)$ 大きい角に対する辺は、小さい角に対する辺より大きい。

[定理 4] 三角形の辺の長さの関係 (補)
$\triangle ABC$で
$(1)$ 二辺の長さの和は、残りの一辺の長さより大きい。
$(2)$ 二辺の長さの差は、残りの一辺の長さより小さい。

[定理 5] (重心) 三角形の中線の交点
三角形の三本の中線は一点で交わり、その交点を$G$とすると、点$G$は三本の中線をそれぞれ$2:1$に内分する。

[定理 6] (内心) 三角形の角の二等分線の交点
三角形の三つの角の二等分線は一点で交わる。

[定理 7] (外心) 三角形の三辺の垂直二等分線の交点
三角形の三辺の垂直二等分線は一点で交わる。

[定理] メネラウスの定理
直線$l$が$\triangle ABC$の三辺$AB,BC,CA$またはその延長と、それぞれ点$P,Q,R$で交わるとき、次の式が成り立つ。
$$\frac{AQ}{QC} \cdot \frac{CP}{PB} \cdot \frac{BR}{RA} =1$$
三角形の辺と交わる場合

三角形の辺の延長線と交わる

[定理] チェバの定理
$\triangle ABC$の頂点$A,B,C$と$1点O$を結ぶ各直線が、大変またはその延長と交わる点をそれぞれ点$P,Q,R$とすると、次の式が成り立つ。
$$\frac{BP}{PC} \cdot \frac{CQ}{QA} \cdot \frac{AR}{RB} =1$$
$1) \ O$が$\triangle ABC$の内部

$2) \ O$が$\triangle ABC$の外部

[定理] (垂心) 三角形の頂点の垂線の交点
三角形の頂点の対辺に対する垂線は一点で交わる。

[定理] (傍心) 三角形の内角の二等分線と外角の二等分線の交点 (補)
三角形の一つの頂点における内角の二等分線と、他の二つの頂点における外角の二等分線は一点で交わる。

[定理 8] 円周角の定理
同じ弧に対する円周角の大きさは等しい。このとき、円周角の大きさはその弧に対する中心角の大きさの半分である。

[定理 9] 円周角の定理の逆
$2点C,P$が直線$AB$について同じ側にあるとき、
$$\angle APB = \angle ACB \iff 4点A,B,C,Pは同じ円周上にある$$

[定理] 円の内部と外部と円周角
円の周上に$3点A,Q,B$があるとき、点$P$が直線$AB$に関して点$Q$と同じ側にあるとき
$(1)$ 点$P$が円の周上にある$\implies \angle APB = \angle AQB$
$(2)$ 点$P$が円の内部にある$\implies \angle APB \gt \angle AQB$
$(3)$ 点$P$が円の内部にある$\implies \angle APB \lt \angle AQB$

[定理] 円に内接する四角形の性質
円に内接する四角形において
$(I)$ 向かい合う内角の和は$180^{\circ}$である。
$(II)$ 一つの内角は、それに向かい合う内角のとなりにある外角に等しい。

[定理] 四角形が円に内接する条件
次のいずれかが成り立つ四角形は円に内接する。
$(I)$ 向かい合う内角の和が$180^{\circ}$の四角形は円に内接する。
$(II)$ 一つの内角が、それに向かい合う内角のとなりにある外角に等しい四角形は円に内接する。

[定理] トレミーの定理
$\square ABCD$が円に内接するとき、対角線$BD$上に$\angle BAE=\angle CAD$となるような点$E$を取るとき、以下が成り立つ。
$$AB \cdot CD + BC \cdot DA = AC \cdot BD$$

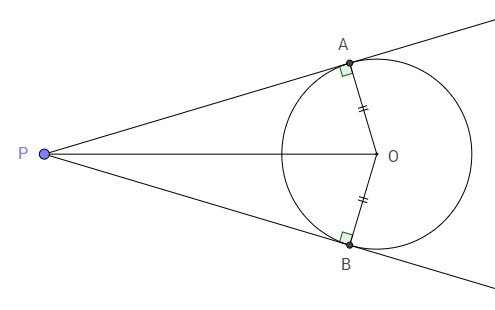
[定理 10] 2本の接線の長さ
円外の点から円にひいた$2$本の接線の長さは等しい。

[定理 11] (接弦定理) 接線と弦のなす角
円の弦$AB$と点$A$における接線$l$とのなす角は、その角の内部にある弧$\stackrel{ \Large \frown }{AB}$に対する円周角$\angle APB$に等しい。

[定理 12] 方冪の定理
$(1)$ 点$P$を通る$2$直線が円とそれぞれ$2点A,B$と$2点C,D$で交わるとき、次の式が成り立つ。
$$PA\cdot PB=PC\cdot PD$$
点$P$が円の内部

点$P$が円の外部

$(2)$ 円外の点$P$を通る$2$直線の一方が円と$2点A,B$で交わり、もう一方が点$T$で接しているとき、次の式が成り立つ。
$$PA\cdot PB=PT^2$$

[定理 13] オイラーの多面体定理
$(頂点の数) - (辺の数) + (面の数) = 2$ または以下のように表す。
$V - E - F = 2$

[定理] 三垂線の定理
平面$\alpha$とその上にない点$A$があり、また$\alpha$上に直線$l$と$l$上にない点$O$がある。$l$上の$1$点を$B$とするとき
$$AB \perp, l \quad OB \perp l, \quad OA \perp OB \implies OA \perp \alpha$$