高校数学 - 三角関数 - きのむくままに

久しぶりに数学を復習しようと思い立ちました。この記事はそのメモです。またLatexで数式を書くための練習です。第8回は三角関数です。第2回三角比で復習した内容を元に比から関数へその考え方を拡張しています。そろそろこのあとの数学で本当に役立つ知識が満載です。

さいんこさいんこさいんさいん、こさいんさいん、たんじぇんと! って「男女」ののりで歌ってる変な人がいたら、それはわたしです(笑

そろそろGeoGebraを使い始めてみます。こんなツールがインターネットで簡単に使えるとか、本当にすごい時代になりましたね。自分の理解をコンピュータで確かめたり、なんとも隔世の感があります。

教材

新編数学II 平成26年度用

編者: 高橋陽一郎
出版社: [啓林館]
発行日: 2013-12-10
ISBN: ISBN978-4-402-04563-0
価格: C4341 ￥00000E

学習範囲 (目次より)
第3章三角関数
第1節一般角の三角関数
1. 一般角
2. 弧度法
3. 一般角の三角関数
4. 三角関数の相互関係
5. 三角関数のグラフ
6. 三角関数を含む方程式・不等式
第2節三角関数の加法定理
1. 三角関数の加法定理
2. 2倍角・半角の公式
3. 三角関数の合成

三角関数

一般角の三角関数

一般角

動径 ( radius vector )・始線 ( initial line )

平面上で定点 $O$ を中心に半直線 $OP$ を回転させ、その回転した角 $\theta$ を考える。
この時回転する半直線 $OP$ を動径といい、その最初の位置 $OX$ を始線という。

動径と始線

角度の正負

時計の針と反対向きに回るとき: 正
時計の針と同じ向きに回るとき: 負

一般角 ( general angle ? )

動径が $1$ 回転以上、すなわち $360^\circ$ 以上回転する場合を考える。回転の向きと大きさを表した角を一般角という。

一般に角 $\alpha$ の動径を $OP$ とすると
$\theta=\alpha+360^\circ\times n (nは整数)$
の角の動径はすべて $OP$ と同じ位置にくる。この角 $\theta$ を動径 $OP$ の表す一般角という。

弧度法

ラジアン ( radian ) 、弧度 ( circular measure, radian )、弧度法 ( radian system )

点 $O$ を中心とする半径 $1$ の円周上の $2$ 点 $A,B$ に対する中心角 $\angle AOB$ の大きさを弧 $AB$ の長さ $\theta$ で表してラジアン、または弧度という単位をつける。
この角の大きさの表し方を弧度法という。

( $\theta=\theta_1=1$ )

$\begin{eqnarray*} 180^\circ&=&\pi[rad]\\ 90^\circ&=&\frac{\pi}{2}[rad]\\ 60^\circ&=&\frac{\pi}{3}[rad]\\ 1^\circ&=&\frac{\pi}{180}[rad] \end{eqnarray*}$
$1[rad]=\frac{180^\circ}{\pi}\fallingdotseq57.3^\circ$
弧度法を用いると角 $\theta$ の動径 $OP$ の表す一般角は下記で表される。
$\theta+2n\pi$

弧度法を用いた扇型の弧の長さと面積

$1$ つの円において扇形のこの長さも面積も中心角の大きさに比例する。半径 $r$ 、中心角 $\theta$ 、扇形のこの長さ $l$ 、面積を $S$ とし、
$\begin{eqnarray*} l&=&r\theta\\ S&=&\frac{1}{2}r^2\theta=\frac{1}{2}rl \end{eqnarray*}$

一般角の三角関数

三角関数 ( trigonometric function )
正弦関数 ( sine function )、余弦関数 ( cosine function )、正接関数 ( tangent function )

一般角 $\theta$ において下記のように定義する。

$\sin\theta=\frac{y}{r}\\ \cos\theta=\frac{x}{r}\\ \tan\theta=\frac{y}{x}$

$\sin$ を正弦、 $\cos$ を余弦、 $tan$ を正接という。

点 $O$ を原点とする座標平面上で $x$ 軸の正の部分を始線とし、角 $\theta$ の同形状に $OP=r$ となる点 $P(x,y)$ をとるとき
$\frac{y}{r},\frac{x}{r},\frac{y}{x}$
を考える。この値は $r$ の大きさに関係なく $\theta$ によって決まる。

一般角における三角比

これらは $\theta$ の関数であり、三角関数という。

単位円

単位円 ( unit circle )

原点 $O$ を中心とする半径 $1$ の円を単位円という。

単位円

三角関数の定義より、 $r=1$ のとき $\sin\theta=y, \cos\theta=x$ であるから、角 $\theta$ の動径と単位円との交点 $P$ の座標は $(\cos\theta, \sin\theta)$ である。
点 $P$ の $x$ 座標、 $y$ 座標の値の範囲は
$-1\le x\le1,-1\le y\le1$
だから
$-1\le \cos\theta\le1,-1\le \sin\theta\le1$
の範囲の値をとる関数である。

三角関数の相互関係

$\begin{align*} &\tan\theta=\frac{\sin\theta}{\cos\theta}\\ &\sin^2\theta+\cos^2\theta=1 tag{1}\\ &1+\tan2\theta=\frac{1}{\cos^2\theta} \end{align*}$

$(1)$ はピタゴラスの定理 ( Pythagorean theorem )。

単位円において角 $\theta$ の動径と単位円との交点を $P(x,y)$ とすると
$x=\cos\theta, y=\sin\theta$
である。 $\tan\theta$ の定義から
$\tan\theta=\frac{y}{x}=\frac{\sin\theta}{\cos\theta}$
である。また $x^2+y^2=1$ であるから
$\cos^2\theta+\sin^2\theta=1$
この式の両辺を $\cos^2\theta$ で割ると
$1+\frac{\sin^2\theta}{\cos^2\theta}=\frac{1}{\cos^2\theta}$

$\displaystyle\tan\theta=\frac{\sin\theta}{\cos\theta}$ だから
$1+\tan^2\theta=\frac{1}{\cos^2\theta}$

三角関数の性質

$\theta+2n\pi$ の三角関数

$\begin{align*} &\sin(\theta+2n\pi)=\sin\theta\\ &\cos(\theta+2n\pi)=\cos\theta\\ &\tan(\theta+2n\pi)=\tan\theta \end{align*}$

単位円において $n$ が整数のとき、角 $\theta+2n\pi$ の動径は角 $\theta$ の動径OPと同じ位置にくる。

$-\theta$ の三角関数 ( reflected )

$\begin{align*} &\sin(-\theta)=-\sin\theta\\ &\cos(-\theta)=\cos\theta\\ &\tan(-\theta)=-\tan\theta \end{align*}$

-θの三角関数

角 $-\theta$ の動径と単位円との交点を $Q$ とするとその座標は
$(\cos(-\theta),\sin(-\theta))$
である。このとき点 $Q$ は点 $P(x,y)$ と $x$ 軸に関して対象で $Q$ の座標は $(x,-y)$ となるから、次の関係が成り立つ。
$\begin{align*} &\sin(-\theta)=-y=-\sin\theta\\ &\cos(-\theta)=x=\cos\theta\\ &\tan(-\theta)=\frac{-y}{x}=-\frac{y}{x}=-\tan\theta \end{align*}$

$\theta+\pi$ の三角関数 ( shift by $\pi$ )

$\begin{align*} &\sin(\theta+\pi)=-\sin\theta\\ &\cos(\theta+\pi)=-\cos\theta\\ &\tan(\theta+\pi)=\tan\theta \end{align*}$

θ+πの三角関数

$\theta+\displaystyle\frac{\pi}{2}$ の三角関数 ( shift by $\displaystyle\frac{\pi}{2}$ )

$\begin{align*} &\sin(\theta+\frac{\pi}{2})=\cos\theta\\ &\cos(\theta+\frac{\pi}{2})=-\sin\theta\\ &\tan(\theta+\frac{\pi}{2})=-\frac{1}{\tan\theta} \end{align*}$

θ+π/2の三角関数

$\pi-\theta, \displaystyle\frac{\pi}{2}-\theta$ の三角関数

$\begin{align*} &\sin(\pi-\theta)=\sin\theta\\ &\cos(\pi-\theta)=-\cos\theta\\ &\tan(\pi-\theta)=-\tan\theta\\ &\sin(\frac{\pi}{2}-\theta)=\cos\theta\\ &\cos(\frac{\pi}{2}-\theta)=\sin\theta\\ &\tan(\frac{\pi}{2}-\theta)=\frac{1}{\tan\theta} \end{align*}$

以上の公式により三角関数は全て鋭角の三角関数で表すことができる。

三角関数のグラフ

$y=\sin\theta$ のグラフ

y=sinθ

$y=\cos\theta$ のグラフ

y=cosθ

周期 ( period )

$\sin(\theta+2\pi)=\sin\theta$ であるから $\sin\theta$ の値は $2\pi$ ごとに同じ変化を繰り返す。この $2\pi$ を $\sin\theta$ の周期という。

周期関数 ( periodic function )

一般に関数 $y=f(\theta)$ が $0$ でない定数 $c$ に対してつねに
$f(\theta+c)=f(\theta)$
となるとき、 $f(\theta)$ は $c$ を周期とする周期関数という。

$y=\tan\theta$ のグラフ

y=tanθ

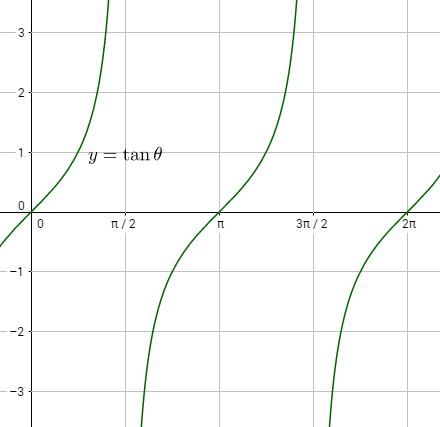
漸近線 ( asymptote )

$\tan\theta$ のグラフでは上下にどこまでものびる曲線で、 $y$ 軸に平行な直線
$\theta=\frac{\pi}{2},\theta=-\frac{\pi}{2},\theta=\frac{3}{2}\pi,\theta=-\frac{3}{2}\pi,\cdots$
に限りなく近づく。このように曲線が限りなく近づいていく直線をその曲線の漸近線という。

三角関数を含む方程式・不等式

練習問題とその解説。略す。

三角関数の加法定理

正弦・余弦の加法定理 ( angle addition theorems )

$\begin{align*} &\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\\ &\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta\\ &\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\\ &\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\\ \end{align*}$

加法定理の証明

半径 $1$ の単位円上に角 $\alpha$ の動径 $OP$ と角 $\beta$ の動径 $OQ$ をとる、点 $P,Q$ の座標はそれぞれ
$P(\cos\alpha, \sin\alpha), Q(\cos\beta, \sin\beta)$
である。このとき余弦定理により
$\begin{align*} PQ^2&=OP^2+OQ^2-2OP\times OQ\cos(\alpha-\beta)\\ &=2-2\cos(\alpha-\beta) \tag{1}\\ \end{align*}$
また $PQ$ 間の距離の $2$ 乗は $2$ 点間の距離より
$\begin{align*} PQ^2&=(\cos\beta-\cos\alpha)^2+(\sin\beta-\sin\alpha)^2\\ &=\cos^2\beta-2\cos\beta\cos\alpha+\cos^2\alpha+\sin^2\beta-2\sin\beta\sin\alpha+\sin^2\alpha\\ &=\sin^2\alpha+\cos^2\alpha+\sin^2\beta+\cos^2\beta-2\cos\beta\cos\alpha-2\sin\beta\sin\alpha\\ &=2-2(\sin\alpha\sin\beta+\cos\alpha\cos\beta) \tag{2} \end{align*}$
$(1), (2)$ より
$2-2\cos(\alpha-\beta)=2-2(\sin\alpha\sin\beta+\cos\alpha\cos\beta)$
よって
$\cos(\alpha-\beta)=\sin\alpha\sin\beta+\cos\alpha\cos\beta \tag{3}$
$(3)$ で、 $\beta$ を $-\beta$ と置き換えて
$\begin{align*} \cos(\alpha+\beta)&=\sin\alpha\sin(-\beta)+\cos\alpha\cos(-\beta)\\ &=\cos\alpha\cos\beta-\sin\alpha\sin\beta \tag{4} \end{align*}$

また、 $\displaystyle\sin\theta=\cos\left(\frac{\pi}{2}-\theta\right), \cos\theta=\sin\left(\frac{\pi}{2}-\theta\right)$ より
$\begin{align*} \sin(\alpha+\beta)&=\cos\left(\frac{\pi}{2}-(\alpha+\beta)\right)\\ &=\cos\left((\frac{\pi}{2}-\alpha)-\beta\right) \end{align*}$
ここで、上記 $(3)$ より
$\begin{align*} \sin(\alpha+\beta)&=\cos\left(\frac{\pi}{2}-\alpha\right)\cos\beta+\sin\left(\frac{\pi}{2}-\alpha\right)\sin\beta\\ &=\sin\alpha\cos\beta+\cos\alpha\sin\beta \tag{5} \end{align*}$

さらに $\beta$ を $-\beta$ におきかえて
$\begin{align*} \sin(\alpha-\beta)&=\sin\alpha\cos(-\beta)+\cos\alpha\sin(-\beta)\\ &=\sin\alpha\cos\beta-\cos\alpha\sin\beta \tag{6} \end{align*}$

正接の加法定理

$\begin{align*} &\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\\ &\tan(\alpha-\beta)=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}\\ \end{align*}$

$\begin{align*} \tan(\alpha+\beta)&=\frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}\\ &=\frac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta} \end{align*}$
ここで、分母分子をそれぞれ $\cos\alpha\cos\beta$ で割ると
$\begin{align*} \tan(\alpha+\beta)&=\frac{\frac{\sin\alpha}{\cos\alpha}+\frac{\sin\beta}{\cos\beta}}{1-\frac{\sin\alpha}{\cos\alpha}\frac{\sin\beta}{\cos\beta}}\\ &=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta} \end{align*}$

上式で $\beta$ の代わりに $-\beta$ とおくと
$\begin{align*} \tan(\alpha-\beta)&=\frac{\sin(\alpha-\beta)}{\cos(\alpha-\beta)}\\ &=\frac{\sin\alpha\cos\beta-\cos\alpha\sin\beta}{\cos\alpha\cos\beta+\sin\alpha\sin\beta} \end{align*}$
ここで、分母分子をそれぞれ $\cos\alpha\cos\beta$ で割ると
$\begin{align*} \tan(\alpha-\beta)&=\frac{\frac{\sin\alpha}{\cos\alpha}-\frac{\sin\beta}{\cos\beta}}{1+\frac{\sin\alpha}{\cos\alpha}\frac{\sin\beta}{\cos\beta}}\\ &=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} \end{align*}$

2直線のなす角

2直線のなす角(1)

直線 $y=mx$ と $x$ 軸の正の部分とのなす角 $\theta$ について $m=\tan\theta$ が成り立っている。このことより $2$ 直線のなす角を導出する。

2直線のなす角(2)

$2$ 直線 $y=mx+n, y=m'x+n'$ のなす角を $\alpha$ とすると $\tan\theta=m, \tan\theta'=m'$ だから $mm'\neq-1$ のとき正接の加法定理により
$\tan\alpha=\tan(\theta'-\theta)=\frac{m'-m}{1+m'm}$
となる。

2倍角・半角の公式

2倍角の公式 ( double-angle formulae )

$\begin{align*} &\sin2\alpha=2\sin\alpha\beta\\ &\cos2\alpha=\cos^2\alpha-\sin^2\alpha=2\cos^2\alpha-1=1-2\sin^2\alpha\\ &\tan2\alpha=\frac{2\tan\alpha}{1-\tan^2\alpha} \end{align*}$

加法定理において $\beta=\alpha$ とおく。

$\begin{align*} \sin(\alpha+\alpha)&=\sin\alpha\cos\alpha+\cos\alpha\sin\alpha\\ &=2\sin\alpha\cos\alpha\\ \cos(\alpha+\alpha)&=\cos\alpha\cos\alpha-\sin\alpha\sin\alpha\\ &=\cos^2\alpha-\sin^2\alpha\\ \tan(\alpha+\alpha)&=\frac{tan\alpha+tan\alpha}{1-\tan\alpha\tan\alpha}\\ &=\frac{2\tan\alpha}{1-\tan^2\alpha} \end{align*}$

半角の公式 ( half-angle formulae )

$\begin{align*} &\sin^2\frac{\alpha}{2}=\frac{1-\cos\alpha}{2}\\ &\cos^2\frac{\alpha}{2}=\frac{1+\cos\alpha}{2} \end{align*}$

余弦の2倍角の公式
$\cos2\alpha=2\cos^2\alpha-1=1-2\sin^2\alpha$
で $\alpha$ を $\displaystyle\frac{\alpha}{2}$ とおく。
$\sin^2\frac{\alpha}{2}=\frac{1-\cos2\alpha}{2}\\ \cos^2\frac{\alpha}{2}=\frac{1+\cos\alpha}{2}$

三角関数の合成

三角関数の合成 ( arbitrary phase shift )

$a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\sin(\theta+\alpha)$
ただし
$\cos\alpha=\frac{a}{\sqrt{a^2+b^2}}, \sin\alpha=\frac{b}{\sqrt{a^2+b^2}}$

三角関数の合成

一般に $a\sin\theta+b\cos\theta$ は以下のように変形できる。
点 $P(a, b)$ をとり、 $x$ 軸の正の部分を始点とする動径 $OP$ の表す角を $\alpha$ とし、 $r=OP=\sqrt{a^2+b^2}$ とすると
$a=r\cos\alpha\\ b=r\sin\alpha$
となる。よって
$\begin{align*} a\sin\theta+b\cos\theta&=r(\cos\alpha\times\sin\theta)+r(\sin\alpha\times\cos\theta)\\ &=r(\sin\theta\cos\alpha+\sin\alpha\cos\theta)\\ &=r\sin(\theta+\alpha) \end{align*}$
となる。これらより
$\begin{align*} a\sin\theta+b\cos\theta&=\sqrt{a^2+b^2}\sin(\theta+\alpha)\\ \cos\alpha&=\frac{a}{r}=\frac{a}{\sqrt{a^2+b^2}}\\ \sin\alpha&=\frac{b}{r}=\frac{b}{\sqrt{a^2+b^2}}\\ \end{align*}$

積和・和積の公式

積和 ( product-to-sum identities )

$\begin{align*} &\sin\alpha\cos\beta=\frac{1}{2}\lbrace\sin(\alpha+\beta)+\sin(\alpha-\beta)\rbrace\\ &\cos\alpha\sin\beta=\frac{1}{2}\lbrace\sin(\alpha+\beta)-\sin(\alpha-\beta)\rbrace\\ &\cos\alpha\cos\beta=\frac{1}{2}\lbrace\cos(\alpha+\beta)+\cos(\alpha-\beta)\rbrace\\ &\sin\alpha\sin\beta=\frac{1}{2}\lbrace\cos(\alpha+\beta)-\cos(\alpha-\beta)\rbrace\\ \end{align*}$

加法定理の公式を加算することで導出可能。

$\begin{align*} \sin(\alpha+\beta)+\sin(\alpha-\beta)&=\sin\alpha\cos\beta+\cos\alpha\sin\beta+\sin\alpha\cos\beta-\cos\alpha\sin\beta\\ &=2\sin\alpha\cos\beta \end{align*}$
これより
$\sin\alpha\sin\beta=\frac{1}{2}\lbrace\sin(\alpha+\beta)+\sin(\alpha-\beta)\rbrace$

和積 ( sum-to-product identities )

$\begin{align*} &\sin A+\sin B=2\sin\frac{A+B}{2}\cos\frac{A-B}{2}\\ &\sin A-\sin B=2\cos\frac{A+B}{2}\sin\frac{A-B}{2}\\ &\cos A+\cos B=2\cos\frac{A+B}{2}\cos\frac{A-B}{2}\\ &\cos A-\cos B=-2\sin\frac{A+B}{2}\sin\frac{A-B}{2} \end{align*}$

積和の公式で、 $\displaystyle\alpha=\frac{A+B}{2},\beta=\frac{A-B}{2}$ と置くことで導出可能。

参考サイト

Qiitaの数式チートシート - Qiita
MathJaxで数式を揃える方法。いままでeqnarray*を使っていましたが、alignを使うのがいいみたいですね。なんで配列出てくるんだろうとおもっていたら行列の表を使っていたんだとわかりました…
加法定理の証明
教科書の加法定理の証明では言葉が足りず、探しました。分かりやすかったです。